Trong hình học, tam giác đều là một dạng hình đặc biệt với nhiều tính chất thú vị. Đặc biệt, việc tính diện tích của tam giác đều không chỉ xuất hiện trong bài tập toán mà còn có thể ứng dụng trong thực tế, kỹ thuật và thiết kế. Nếu bạn đang tìm cách tính diện tích tam giác đều một cách đơn giản, bài viết sau sẽ giúp bạn hiểu cặn kẽ và áp dụng chính xác. Trong hình học phẳng, hình tam giác là một đa giác đơn giản bao gồm ba cạnh nối liền ba đỉnh không thẳng hàng. Mỗi cặp cạnh gặp nhau tại một điểm gọi là đỉnh và các đoạn thẳng nối giữa các đỉnh chính là các cạnh của tam giác. Một đặc điểm nổi bật của tam giác là: tổng số đo ba góc bên trong luôn bằng 180 độ. Nhờ vào tính chất hình học cơ bản này, tam giác là nền tảng quan trọng trong các định lý, bài toán và ứng dụng thực tế trong thiết kế, kiến trúc, và cả trong lập trình máy tính. Việc phân biệt các dạng tam giác không chỉ giúp xác định công thức tính diện tích chính xác, mà còn giúp bạn làm quen với các dạng bài tập hình học đa dạng trong chương trình học. Như đã nói ở trên, đây là loại tam giác có ba cạnh bằng nhau và ba góc bằng nhau. Mỗi góc của tam giác đều đều có giá trị 60 độ. Nhờ đặc điểm đối xứng này, tam giác đều mang lại nhiều lợi thế khi áp dụng các công thức hình học. Ngoài việc phổ biến trong sách giáo khoa, hình tam giác đều còn hiện diện trong thiết kế, kiến trúc, kỹ thuật và cả mỹ thuật, nhờ tính cân đối và dễ thao tác tính toán. Trong hình học, tam giác đều là một dạng đặc biệt của tam giác, nơi mà cả ba cạnh đều có độ dài bằng nhau và mỗi góc bên trong đều bằng 60 độ. Nhờ vào tính đối xứng hoàn hảo này, việc tính diện tích tam giác đều trở nên đơn giản và nhanh chóng hơn nhiều so với các loại tam giác thông thường. Dưới đây là các cách phổ biến để tính diện tích tam giác đều tùy theo dữ kiện đề bài cung cấp: Nếu bạn chỉ biết độ dài một cạnh của tam giác đều, hoàn toàn có thể xác định chiều cao bằng cách kẻ một đường thẳng nối từ đỉnh đến đáy. Đường cao này sẽ vuông góc với cạnh đối diện và đồng thời chia cạnh đó thành hai phần bằng nhau tại trung điểm. Khi đó, bạn có thể vận dụng định lý Pythagoras (a² + b² = c²) để tính chiều cao dựa trên tam giác vuông được tạo thành. Sau khi có được chiều cao, việc áp dụng công thức diện tích tam giác theo chiều cao trở nên đơn giản: Tuy nhiên, để tính nhanh và tiết kiệm thời gian hơn, bạn có thể sử dụng trực tiếp công thức đặc biệt dành riêng cho tam giác đều sau: Ví dụ minh họa: Trong một số bài toán, thay vì chỉ cho độ dài cạnh, đề bài có thể cung cấp thêm chiều cao tương ứng từ đỉnh tới đáy. Khi đó, bạn hoàn toàn có thể sử dụng công thức diện tích tam giác tổng quát để tính: Trong đó: Cách tính này vẫn hoàn toàn chính xác và linh hoạt, đặc biệt hữu ích trong các bài toán thực tế hoặc đề không yêu cầu áp dụng công thức đặc biệt. Nếu muốn kiểm tra lại kết quả hoặc không nhớ công thức nhanh, bạn có thể dùng cách này để thay thế hiệu quả. Ví dụ minh họa: Ngoài việc tìm diện tích, đôi khi bài toán sẽ yêu cầu bạn xác định chiều cao của tam giác đều. Trong trường hợp đó, bạn cần nắm rõ đặc điểm và công thức liên quan đến đường cao trong tam giác đều. Đặc điểm của đường cao trong tam giác đều: Nếu bạn đã biết độ dài một cạnh của tam giác đều, có thể tính nhanh chiều cao bằng công thức: Trong đó: Công thức này giúp bạn dễ dàng suy ra chiều cao mà không cần phải vẽ hình hay sử dụng định lý Pythagoras, đặc biệt hữu ích trong các bài toán yêu cầu tính diện tích gián tiếp hoặc thiết kế hình học. Ví dụ minh họa: Tham khảo thêm công thức tính thể tích khối nón để nắm chắc cách tính nhanh cho các bài toán hình học nhé. Tam giác đều không chỉ là bài toán trên giấy. Trong đời sống, tam giác đều xuất hiện ở: Qua những thông tin đã trình bày, chắc hẳn bạn đã hiểu rõ diện tích tam giác đều là gì, cách phân biệt tam giác đều với các loại tam giác khác và áp dụng công thức một cách chính xác. Dù đơn giản, nhưng kiến thức này là nền tảng cho nhiều chuyên đề toán học khác. Nếu bạn đang tìm thiết bị hỗ trợ học tập trực tuyến như máy tính bảng, điện thoại hay laptop sinh viên, đừng quên FPT Shop luôn có sẵn nhiều lựa chọn chính hãng, giá tốt và tư vấn tận tình! Xem thêm:Hình tam giác là gì?

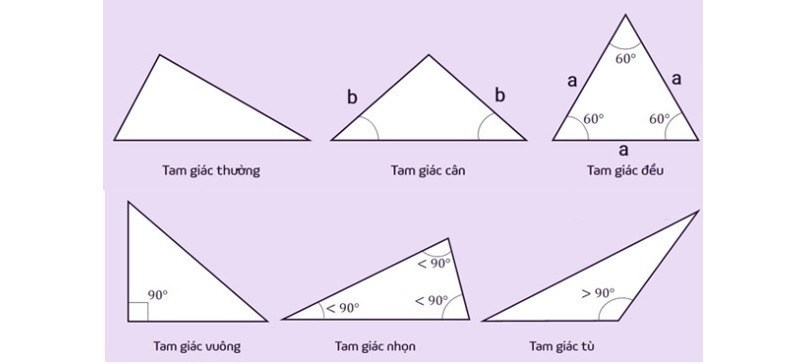
Các loại tam giác trong hình học
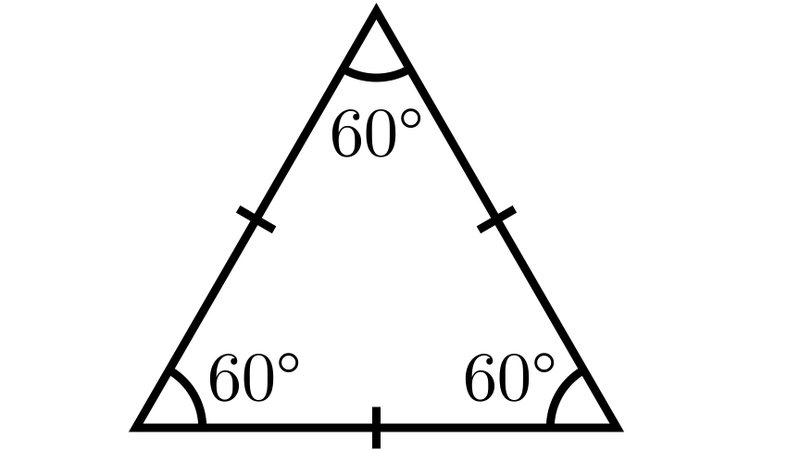
Hình tam giác đều là gì?
Các cách tính diện tích tam giác đều
Trường hợp cho chiều dài của cạnh


Trường hợp biết chiều dài một cạnh và chiều cao tương ứng
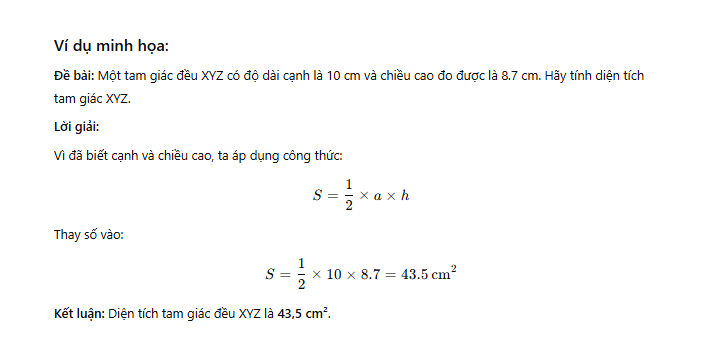
Trường hợp yêu cầu tính chiều cao của tam giác đều

Ứng dụng của tam giác đều trong thực tế

Kết bài

Cách tính diện tích tam giác đều nhanh chóng, đơn giản hữu ích dành cho bạn
- 70,000
- Tác giả: admin
- Ngày đăng: 03:40 18/12/2025
- Lượt xem: 7
- Tình trạng: Còn hàng