Hình thang là một trong những hình học cơ bản và không còn xa lạ với hầu hết mọi người. Tuy nhiên, không phải ai cũng nhớ được công thức tính diện tích hình thang một cách chính xác và dễ hiểu. Tuy nhiên đừng quá lo lắng, vì bài viết dưới đây của FPT Shop sẽ giúp bạn nắm vững công thức tính diện tích hình thang cân, vuông,... và 4 lưu ý quan trọng khi làm các dạng bài tập liên quan. Trước khi đi vào công thức tính diện tích hình thang, chúng ta hãy cùng nhắc lại định nghĩa của hình thang để hiểu rõ hơn. Hình thang là một tứ giác có hai cạnh đối song song với nhau, trong đó hai cạnh song song được gọi là các cạnh đáy (đáy lớn và đáy nhỏ), hai cạnh còn lại được gọi là các cạnh bên. Tùy thuộc vào tính chất của cạnh bên và góc giữa các cạnh, hình thang thường được chia thành ba loại chính: Sau khi đã hiểu hình thang là gì, hãy cùng đi đến phần quan trọng nhất của bài viết: công thức tính diện tích hình thang. Cụ thể, diện tích của hình thang được tính dựa trên độ dài của hai cạnh đáy và chiều cao của hình thang. Để tính diện tích hình thang, bạn sẽ lấy chiều dài 2 cạnh đáy cộng lại với nhau, sau đó tất cả nhân cho chiều cao rồi chia cho 2: S =[(a+b)*h]/2 Trong đó: Ví dụ: Giả sử, bạn có một hình thang với độ dài của đáy lớn là 10cm, đáy nhỏ là 6cm và chiều cao là 5cm. Bạn có thể áp dụng công thức tính diện tích hình thang như sau: S=[(10+6)*5]/2=(16*5)/2=40cm². Vậy diện tích của hình thang trong trường hợp này là 40cm². Ở Việt Nam, khi học toán, nhiều bạn thường gặp khó khăn trong việc nhớ các công thức hình học, đặc biệt là công thức tính diện tích hình thang. Tuy nhiên, có một cách rất đơn giản, dễ thuộc để ghi nhớ, đó chính là thông qua những bài thơ vần điệu. Một trong những bài thơ giúp học sinh nhớ nhanh và chính xác công thức tính diện tích hình thang đã được nhiều người thuộc nằm lòng: "Muốn tính diện tích hình thang Đáy lớn, đáy nhỏ ta mang cộng vào Rồi đem nhân với chiều cao Chia đôi lấy nửa, thế nào cũng ra." Cách học bằng thơ này đặc biệt hữu ích ở Việt Nam, nơi mà phương pháp học thuộc qua vần điệu rất phổ biến và dễ áp dụng. Đây là mẹo học vừa hiệu quả, vừa gần gũi với nhiều thế hệ học sinh Việt. Khi bạn gặp bài toán liên quan đến diện tích hình thang, chỉ cần nhớ lại bài thơ này là có thể tự tin giải quyết bài tập một cách nhanh chóng. Hình thang vuông là hình thang có một góc vuông giữa cạnh bên và một trong hai cạnh đáy. Trong trường hợp này, cách tính diện tích vẫn sử dụng công thức tính diện tích hình thang chung, không có sự khác biệt lớn. Ví dụ, với một hình thang vuông có đáy lớn là 8cm, đáy nhỏ là 4cm và chiều cao là 3cm, diện tích được tính như sau: S=[(8+4)*3]/2=(12*3)/2=18cm2 Hình thang cân là hình thang có hai cạnh bên bằng nhau. Để tính diện tích hình thang cân, bạn cũng áp dụng công thức tính diện tích hình thang như trên, vì chiều cao vẫn được xác định là khoảng cách vuông góc giữa hai cạnh đáy. Nếu hình thang có hai cạnh bên và góc tạo thành giữa một cạnh bên và đáy, bạn có thể sử dụng định lý Pytago để tính chiều cao. Định lý Pytago quy định: Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông. Định lý Pytago thường áp dụng trong hình thang vuông hoặc hình thang có thể chia thành hai tam giác vuông. Dưới đây là công thức tính diện tích hình thang dựa trên định lý Pytago: h2 = c2 - [(a-b)/2]2 Trong đó Sau khi tính được chiều cao, bạn có thể áp dụng công thức tính diện tích hình thang như thông thường. Dưới đây là một số bài tập tính diện tích hình thang giúp bạn ôn luyện và củng cố kiến thức: Các bài tập này sẽ giúp bạn làm quen với nhiều dạng câu hỏi và nắm vững cách áp dụng công thức tính diện tích hình thang trong nhiều tình huống khác nhau. Khi tính diện tích hình thang, ngoài việc áp dụng đúng công thức, bạn cũng cần lưu ý một số điểm quan trọng để tránh sai sót. Và dưới đây là 4 lưu ý quan trọng nhất bạn không nên bỏ qua khi tính toán: Tạm kết Như vậy, việc nắm vững công thức tính diện tích hình thang và 4 lưu ý quan trọng đã được đề cập sẽ giúp bạn tránh những sai lầm phổ biến, từ việc xác định chiều cao, đáy cho đến áp dụng công thức chính xác. Đừng quên luyện tập nhiều dạng bài tập để nâng cao kỹ năng của mình nhé! Ngoài ra, nếu bạn đang tìm kiếm một chiếc laptop hiệu năng cao để học tập và làm việc mượt mà, hãy tham khảo ngay các mẫu laptop tại FPT Shop. Với tốc độ xử lý mạnh mẽ, laptop sẽ là trợ thủ đắc lực cho việc học của bạn! Xem ngay tại đây nhé! Laptop giá rẻ Xem thêm:Hình thang là gì?

Công thức tính diện tích hình thang
Mẹo nhớ công thức tính diện tích hình thang

Công thức tính diện tích hình thang trong các trường hợp đặc biệt
Diện tích hình thang vuông
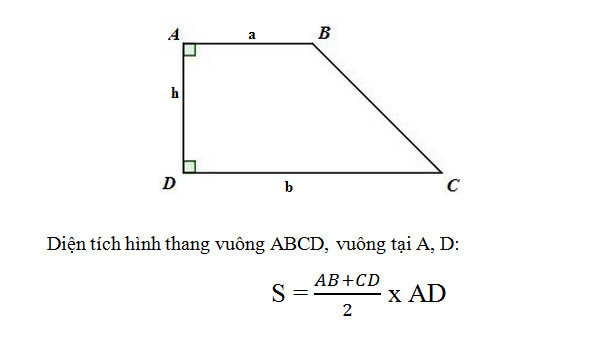
Diện tích hình thang cân
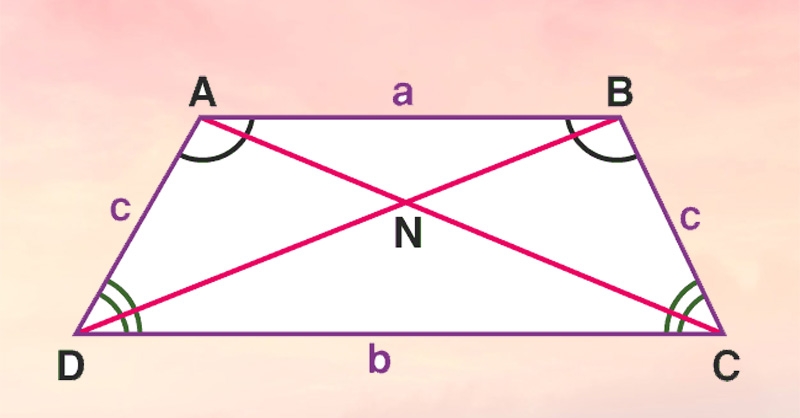
Cách tính diện tích hình thang khi không biết chiều cao

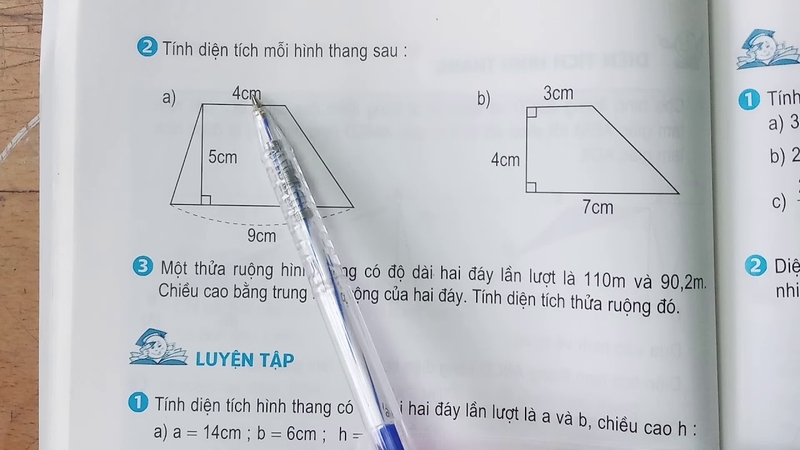
Một số dạng bài tập tính diện tích hình thang phổ biến
4 lưu ý khi tính diện tích hình thang

Công thức tính diện tích hình thang: thường, cân, vuông và ví dụ minh họa dễ hiểu
- 90,000
- Tác giả: admin
- Ngày đăng: 01:30 18/12/2025
- Lượt xem: 9
- Tình trạng: Còn hàng