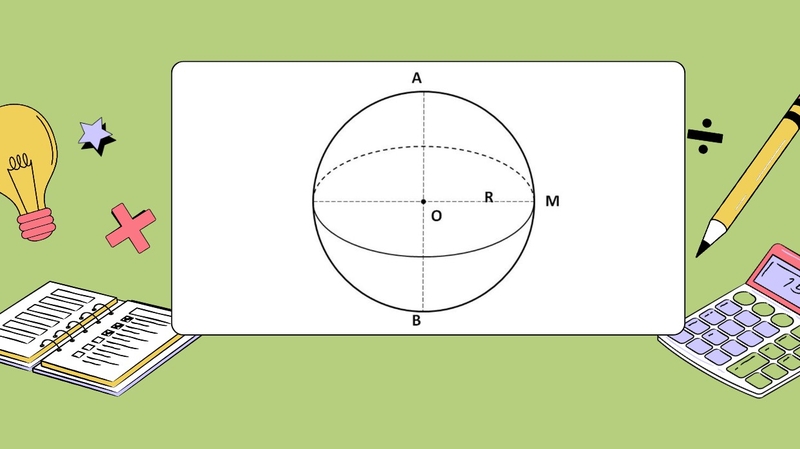
Hình cầu là một dạng hình học quen thuộc, hiện diện khắp mọi nơi trong cuộc sống, từ những quả bóng nhỏ xinh đến các hành tinh rộng lớn trong không gian. Nhưng bạn đã bao giờ tự hỏi cách tính thể tích của hình cầu như thế nào chưa? Trong bài viết này của FPT Shop sẽ giúp bạn khám phá chi tiết về hình cầu, các tính chất đặc trưng và đặc biệt là công thức tính thể tích hình cầu thông qua những ví dụ minh họa dễ hiểu. Hình cầu là một hình học ba chiều được tạo ra khi nửa hình tròn quay tròn quanh đường kính của nó. Cụ thể, nếu bạn lấy một nửa hình tròn với tâm O và bán kính R, sau đó xoay nó một vòng quanh trục đường kính AB cố định trong không gian, bạn sẽ thu được một hình cầu. Trong hình cầu này, điểm O được gọi là tâm, còn R là bán kính của hình cầu hoặc mặt cầu đó. Thể tích hình cầu là đại lượng biểu thị không gian ba chiều mà hình cầu chiếm giữ. Với cấu trúc đặc biệt, mọi điểm trên bề mặt hình cầu đều cách tâm một khoảng không đổi, tạo nên sự cân đối hoàn hảo. Để dễ hình dung, bạn có thể liên tưởng đến những vật thể quen thuộc trong cuộc sống. Hãy nghĩ đến một quả bóng tròn. Không gian bên trong quả bóng chính là thể tích mà quả bóng đó chiếm giữ. Hình cầu có hai tính chất quan trọng như sau: Trước khi tìm hiểu công thức tính thể tích hình cầu, hãy cùng làm rõ một số khái niệm quan trọng liên quan. Xem ngay các giải thích chi tiết dưới đây để nắm rõ những thông tin cần thiết. Mặt cầu chỉ bao gồm bề mặt cong tròn, không chứa phần không gian bên trong. Để dễ hình dung, bạn có thể tưởng tượng đến lớp vỏ mỏng của một quả bóng bay căng tròn. Lớp vỏ đó chính là mặt cầu, chỉ là một bề mặt cong và rỗng, không có bất kỳ phần nào bên trong. Để hiểu rõ hơn về hình học không gian, bạn có thể quan sát các vật thể thực tế xung quanh và tập đo lường, tính toán bằng cách sử dụng một chiếc máy tính cầm tay hiện đại. Công cụ này sẽ trở thành trợ thủ đắc lực, giúp bạn tính toán và học tập dễ dàng hơn. Nếu mặt cầu chỉ là lớp vỏ mỏng bao quanh, thì khối cầu chính là toàn bộ phần không gian nằm bên trong lớp vỏ đó. Đơn giản hơn, bạn có thể tưởng tượng khối cầu giống như một quả bóng đặc, chứa đầy vật chất bên trong. Một ví dụ dễ hiểu là quả bóng đá: lớp vỏ da bên ngoài đại diện cho mặt cầu, còn không khí bơm căng bên trong là phần khối cầu. Tương tự, viên bi thủy tinh hoặc kim loại đặc cũng là một ví dụ minh họa trực quan về khối cầu. Thể tích hình cầu, hay còn gọi là thể tích khối cầu, được tính bằng cách lấy 4/3 nhân với hằng số Pi và nhân tiếp với bán kính của hình cầu nâng lên lũy thừa ba. Công thức: 4/3 x π x R³ Trong công thức: Xác định các dữ kiện được cung cấp, chẳng hạn như bán kính (R) hoặc đường kính (D) của hình cầu. Kiểm tra và chuyển đổi đơn vị đo lường nếu cần thiết (ví dụ: từ cm sang m). Sử dụng công thức tính thể tích khối cầu: Nếu đề bài cung cấp đường kính (D), tính bán kính bằng công thức: Bước 3: Thay số và tính toán Thay giá trị bán kính (R) vào công thức trên. Sử dụng máy tính hoặc thực hiện các phép toán để tính kết quả. Bước 4: Kiểm tra kết quả Đánh giá tính hợp lý của kết quả dựa trên dữ kiện bài toán và đơn vị đo lường đã sử dụng. Đảm bảo kết quả chính xác, không có sai sót trong quá trình tính toán. Khi giải bài tập về thể tích hình cầu, bạn thường gặp các tình huống sau: Hình cầu kết hợp với hình khối khác: Trong một số bài tập phức tạp, hình cầu có thể nội tiếp hoặc ngoại tiếp các hình khối khác như hình lập phương hay hình trụ. Khi đó, bạn cần dựa vào mối quan hệ hình học giữa các hình để tìm bán kính của hình cầu, từ đó tính được thể tích. Bài tập 1 Cho một hình cầu có bán kính R = 5 cm. Hãy tính thể tích của khối cầu. Lời giải Cho bán kính R=5cm. Thay R = 5cm vào công thức Thể tích khối cầu: V = (4/3)πR³ = (4/3)π(5)³ = (500/3)π Với π ≈ 3,14159 V = (500/3) x 3,14159 = 523,60 cm3 Vậy thể tích khối cầu là 523.60 cm³ Bài tập 2 Một quả bóng đá có đường kính 30 cm. a) Xác định bán kính của quả bóng đá. b) Tính thể tích khối cầu của quả bóng đá. Lời giải a) Xác định bán kính của quả bóng đá Công thức tính bán kính: R = D/2 R = 30/2 = 15cm Bán kính của quả bóng đá là:15 cm b) Tính thể tích khối cầu của quả bóng đá Công thức thể tích khối cầu: V = (4/3)πR³ Thay R = 15cm vào công thức Thể tích khối cầu: V = (4/3)πR³ = (4/3)π(15)³ = (13500/3)π = 4500π Với π ≈ 3,14159 V = (500/3) x 3,14159 = 14.137,17 cm³ Thể tích khối cầu là: 14.137,17 cm³ Công thức tính thể tích hình cầu, tuy đơn giản, lại mang đến những ứng dụng thực tiễn và khoa học đa dạng: Hy vọng qua bài viết trên, bạn đã hiểu rõ về công thức tính thể tích hình cầu và cách áp dụng nó. Những phương pháp được chia sẻ sẽ giúp bạn dễ dàng giải quyết các bài tập cũng như các vấn đề thực tế liên quan. Đừng quên truy cập FPT Shop để khám phá thêm nhiều kiến thức bổ ích và ứng dụng thú vị khác nhé. Bạn đang tìm kiếm một chiếc điện thoại với hiệu năng mạnh mẽ, thiết kế hiện đại và giá cả hợp lý? Xiaomi chính là lựa chọn hoàn hảo dành cho bạn! Ghé ngay FPT Shop để khám phá các dòng sản phẩm Xiaomi mới nhất cùng những ưu đãi hấp dẫn. Đừng bỏ lỡ cơ hội sở hữu chiếc smartphone Xiaomi yêu thích với chế độ bảo hành chính hãng và dịch vụ chăm sóc tận tâm tại FPT Shop. Xem thêmThế nào là hình cầu?

Định nghĩa thể tích hình cầu
Tính chất của hình cầu
Một số khái niệm khác liên quan về thể tích hình cầu
Mặt cầu
Khối cầu
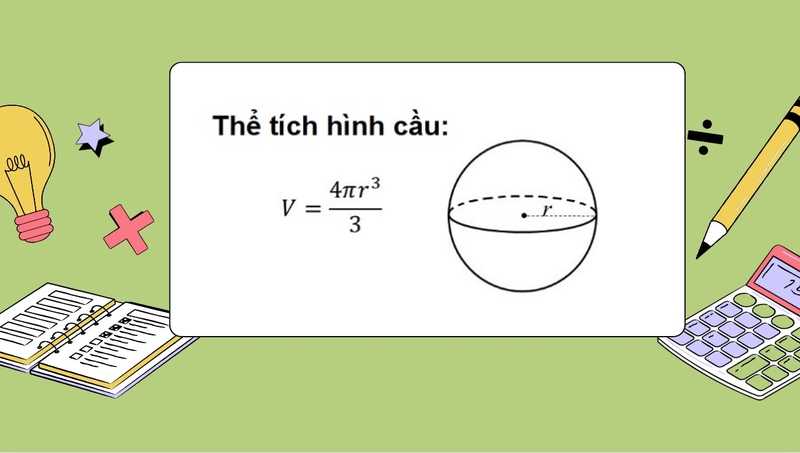
Công thức tính thể tích hình cầu
Hướng dẫn các bước giải bài tập tính thể tích khối cầu
Bước 1: Phân tích đề bài
Bước 2: Lựa chọn công thức
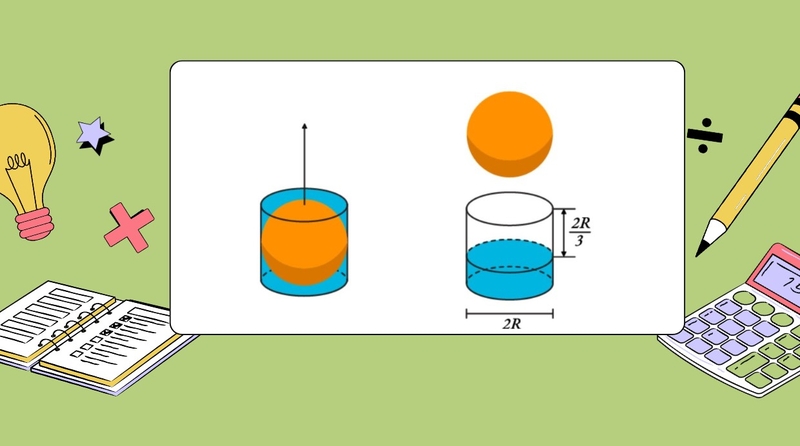
Các dạng bài tập hình cầu thường gặp
Một số bài tập tính thể tích khối cầu
Ứng dụng của công thức tính thể tích hình cầu

Lời kết

Công thức tính thể tích hình cầu, các dạng bài tập và các ứng dụng hữu ích trong cuộc sống
- 60,000
- Tác giả: admin
- Ngày đăng: 12:30 21/12/2025
- Lượt xem: 6
- Tình trạng: Còn hàng