Hiểu rõ công thức tính thể tích hình trụ sẽ giúp bạn giải quyết nhiều bài toán thực tiễn liên quan đến việc đo lường và tính toán không gian. Trong bài viết này, hãy cùng FPT Shop tìm hiểu chi tiết công thức tính thể tích hình trụ. Hình trụ là một trong những hình học cơ bản mà chúng ta thường gặp trong đời sống và nhiều ngành công nghiệp. Một hình trụ được hình thành khi một mặt phẳng tròn được kéo dài ra theo một chiều dọc, tạo thành một cấu trúc ba chiều có hai đáy tròn và một mặt bên phẳng. Để hiểu rõ hơn về các ứng dụng của hình trụ, việc nắm vững cách tính thể tích của nó là vô cùng quan trọng. Thể tích của hình trụ biểu thị phần mà hình trụ chiếm giữ trong không gian ba chiều, được tính bằng cách nhân diện tích đáy tròn với chiều cao của hình trụ. Công thức tính thể tích hình trụ không chỉ quan trọng trong các bài toán học mà còn có ứng dụng rất rộng rãi trong các lĩnh vực khác nhau như xây dựng, công nghiệp và ngay cả trong đời sống hàng ngày. Từ việc đo lường thể tích bể chứa nước, đến tính toán các không gian lưu trữ trong công nghiệp, hay đơn giản hơn là ước lượng dung tích của một lon nước giải khát, công thức này có thể được sử dụng ở nhiều tình huống khác nhau. V=π×r2 ×h Trong đó: Giả sử chúng ta có một hình trụ với bán kính đáy là 5 cm và chiều cao là 10 cm. Chúng ta sẽ áp dụng công thức tính thể tích hình trụ để tìm thể tích của hình này. Bước 1: Xác định các giá trị cần thiết. Bước 2: Áp dụng công thức Vậy thể tích của hình trụ này là 785,4 cm³. Công thức tính thể tích hình trụ có rất nhiều ứng dụng thực tế trong cuộc sống, đặc biệt trong các ngành công nghiệp và xây dựng. Dưới đây là một số ví dụ điển hình: Mặc dù công thức tính thể tích hình trụ là một trong những công thức khá cơ bản trong toán học, nhưng thực tế khi áp dụng vào các bài toán thực tế, nhiều người vẫn dễ mắc phải các sai lầm dẫn đến kết quả sai lệch. Dưới đây là một số sai lầm thường gặp khi tính thể tích hình trụ mà bạn cần lưu ý. Đây có lẽ là lỗi phổ biến nhất khi tính toán thể tích hình trụ, đặc biệt là đối với những người mới làm quen với hình học không gian. Chiều cao và bán kính đều là những thông số quan trọng trong công thức tính thể tích, nhưng nếu bạn nhầm lẫn giữa hai đại lượng này, kết quả sẽ bị sai lệch nghiêm trọng. Trong công thức tính thể tích hình trụ, bán kính (r) là khoảng cách từ tâm của đáy trụ đến cạnh ngoài, trong khi chiều cao (h) là khoảng cách giữa hai mặt đáy. Nếu nhầm lẫn giữa chiều cao và bán kính, kết quả tính toán sẽ không chính xác vì diện tích đáy phụ thuộc vào r2, còn thể tích được xác định dựa trên nhân với chiều cao. Một trong những yếu tố quan trọng khi tính toán thể tích của bất kỳ hình tròn nào, bao gồm hình trụ, là giá trị của số pi (π). Pi là một hằng số toán học có giá trị xấp xỉ bằng 3,14159. Tuy nhiên, trong nhiều trường hợp, người học có thể sử dụng các giá trị pi không chính xác, chẳng hạn như làm tròn quá mức hoặc sử dụng các ước lượng không hợp lý. Điều này có thể dẫn đến sai số, đặc biệt là khi tính toán thể tích với các hình trụ có kích thước lớn. Nếu không tính toán chính xác giá trị của pi, kết quả cuối cùng sẽ không đảm bảo tính chính xác. Một lỗi khác mà nhiều người thường gặp phải là quên hoặc sử dụng không chính xác đơn vị đo khi tính thể tích. Thể tích được đo bằng đơn vị lập phương (cm³, m³, vv.), nhưng nếu người tính toán không chuyển đổi đúng giữa các đơn vị đo chiều dài, bán kính, và chiều cao, kết quả sẽ không phù hợp với yêu cầu thực tế. Ví dụ, nếu chiều cao được tính bằng mét và bán kính tính bằng centimet, nhưng không chuyển đổi đơn vị trước khi áp dụng vào công thức, kết quả thể tích sẽ không khớp với đơn vị lập phương mà đề bài yêu cầu. Để đảm bảo việc tính toán thể tích hình trụ nhanh chóng và chính xác, người học nên áp dụng một số mẹo và phương pháp sau: Sử dụng máy tính hoặc các ứng dụng tính toán trực tuyến sẽ giúp bạn tránh được nhiều sai sót khi thực hiện các phép tính phức tạp liên quan đến số pi và số mũ. Điều này đặc biệt hữu ích khi bạn cần thực hiện nhiều phép tính với độ chính xác cao mà không cần phải thực hiện tất cả các bước tính tay. Hiện nay, nhiều công cụ trực tuyến còn cung cấp chức năng tính thể tích hình trụ chỉ bằng cách nhập các thông số như bán kính và chiều cao. Khi làm các bài toán thực tế, không phải lúc nào bạn cũng cần kết quả với độ chính xác tuyệt đối. Trong nhiều trường hợp, bạn có thể làm tròn kết quả để dễ hiểu hơn và phù hợp với ngữ cảnh bài toán. Tuy nhiên, bạn cần lưu ý làm tròn một cách hợp lý, đặc biệt khi tính toán các phép toán liên quan đến số pi (π), để tránh sai lệch quá lớn. Chọn đúng đơn vị đo là yếu tố cực kỳ quan trọng khi tính toán thể tích hình trụ. Trước khi bắt đầu tính toán, bạn cần đảm bảo rằng tất cả các đại lượng được đo bằng cùng một đơn vị, đặc biệt là đối với chiều cao và bán kính. Ngoài ra, việc sử dụng các đơn vị phù hợp với ngữ cảnh bài toán (ví dụ: sử dụng mét khối cho các công trình xây dựng lớn, hoặc lít cho dung tích bể chứa nước) sẽ giúp kết quả tính toán trở nên thực tế hơn. Công thức tính thể tích hình trụ là một kiến thức cơ bản nhưng rất quan trọng trong toán học và nhiều lĩnh vực khác. Nắm vững công thức này sẽ giúp bạn giải quyết các bài toán một cách nhanh chóng và có thể ứng dụng trong nhiều tình huống thực tiễn như xây dựng, công nghiệp, và đời sống hàng ngày. Tại FPT Shop, bạn sẽ tìm thấy nhiều mẫu laptop giá tốt dành riêng cho học sinh, sinh viên, phù hợp với nhu cầu học tập và giải trí. Đừng bỏ lỡ cơ hội sở hữu những thiết bị chất lượng với mức giá ưu đãi. Hãy ghé thăm FPT Shop ngay hôm nay để lựa chọn cho mình một chiếc laptop ưng ý và tận hưởng các chương trình khuyến mãi hấp dẫn. Xem thêm về laptop giá tốt tại đây: Xem thêm:Giới thiệu về hình trụ

Công thức tính thể tích hình trụ
Công thức
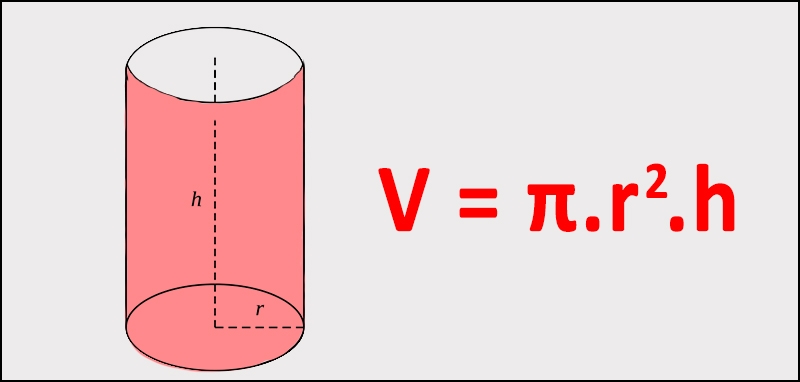
Ví dụ minh họa

Ứng dụng thực tế của công thức tính thể tích hình trụ

Các sai lầm thường gặp khi tính thể tích hình trụ
Nhầm lẫn giữa chiều cao (h) và bán kính đáy (r)

Không tính chính xác giá trị của số pi (π)
Quên đơn vị đo
Mẹo tính toán nhanh và chính xác
Sử dụng máy tính
Làm tròn kết quả một cách hợp lý
Chọn đơn vị đo phù hợp
Tạm kết
Công thức tính thể tích hình trụ: Giải thích chi tiết, ví dụ minh họa và ứng dụng thực tế trong đời sống
- 110,000
- Tác giả: admin
- Ngày đăng: 09:20 18/12/2025
- Lượt xem: 11
- Tình trạng: Còn hàng