Trong toán học tập, định nghĩa khoảng cách đằm thắm hai tuyến phố trực tiếp vào vai trò cần thiết trong những công việc xử lý những câu hỏi hình học tập kể từ cơ bạn dạng cho tới nâng lên. Dù chúng ta đang được học tập về hình học tập phẳng lặng hoặc tò mò không khí phụ thân chiều, việc đo lường khoảng cách đằm thắm hai tuyến phố trực tiếp vẫn là một khả năng quan trọng. Vì vậy, tất cả chúng ta hãy nằm trong lần hiểu phương pháp tính khoảng cách đằm thắm hai tuyến phố trực tiếp vô hình học tập phẳng lặng và không khí nhằm chúng ta cũng có thể vận dụng những cách thức này trong những trường hợp thực tiễn và vô tiếp thu kiến thức.
Cách tính khoảng cách đằm thắm hai tuyến phố trực tiếp vô hình học tập phẳng
Để tính khoảng cách đằm thắm hai tuyến phố trực tiếp vô hình học tập phẳng lặng, các bạn sẽ cần phải biết Đặc điểm và công thức tính.
1. Đặc điểm của hai tuyến phố thẳng
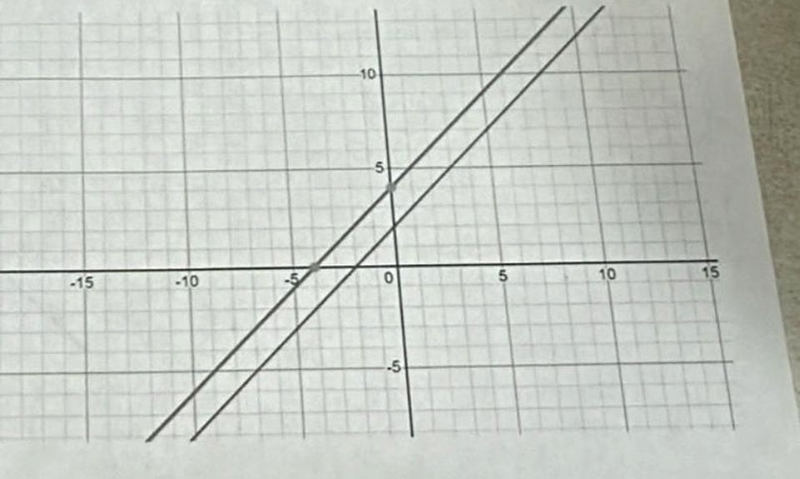
Trong hình học tập phẳng lặng, hai tuyến phố trực tiếp rất có thể với phụ thân quan hệ chính:
- Song song: Hai đường thẳng liền mạch tuy vậy song là khi nó không giao phó nhau bên trên ngẫu nhiên điểm nào là, tức là những thông số của x và nó vô phương trình tổng quát mắng của nó có nằm trong tỷ trọng, tuy nhiên thông số tự tại không giống nhau. Ví dụ: hai tuyến phố trực tiếp với dạng Ax + By + C1 = 0 và Ax + By + C2 = 0 là tuy vậy song nếu như A/B = A/B, tuy nhiên C1 ≠ C2.
- Cắt nhau: Hai đường thẳng liền mạch rời nhau khi nó với cùng một nút giao nhau có một không hai. Như vậy xẩy ra Lúc những thông số của x và nó vô phương trình của nó không tồn tại nằm trong tỷ trọng, tức là nếu như phương trình của nó với dạng Ax + By + C = 0 và A′x + B′y +C′ = 0, thì A/B ≠ A′/B′.
- Trùng nhau: Đây là tình huống đặc trưng của đường thẳng liền mạch tuy vậy tuy vậy, Lúc bọn chúng với những thông số trọn vẹn tương đương nhau và nằm trong trải qua từng điểm.
2. Công thức tính khoảng cách đằm thắm hai tuyến phố trực tiếp tuy vậy song
Để tính khoảng cách đằm thắm hai tuyến phố trực tiếp tuy vậy song vô mặt mũi phẳng lặng, chúng ta cũng có thể dùng công thức như sau:
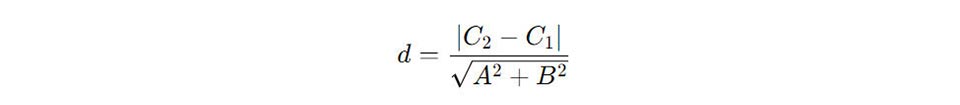
Trong đó:
- A và B là những thông số của x và nó vô phương trình tổng quát mắng của hai tuyến phố trực tiếp.
- C1 và C2 là những thông số tự tại của hai tuyến phố trực tiếp tuy vậy tuy vậy.
Ví dụ: với hai tuyến phố trực tiếp 3x + 4y + 5 = 0 và 3x + 4y – 7 = 0, khoảng cách giữa 2 đường thẳng liền mạch này sẽ tiến hành tính là:
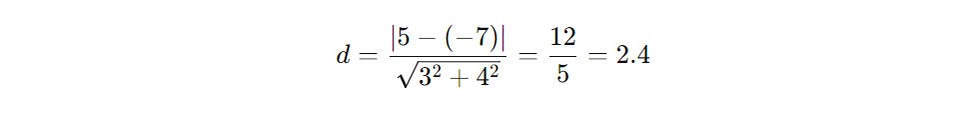
Điều này đã cho chúng ta thấy khoảng cách đằm thắm hai tuyến phố trực tiếp tuy vậy song thực tế là khoảng cách vuông góc từ 1 điểm ngẫu nhiên bên trên một đường thẳng liền mạch cho tới đường thẳng liền mạch còn lại.
3. Cách tính khoảng cách đằm thắm hai tuyến phố trực tiếp rời nhau
Đối với hai tuyến phố trực tiếp rời nhau, không tồn tại khoảng cách thắt chặt và cố định đằm thắm bọn chúng vì thế bọn chúng giao phó nhau bên trên một điểm có một không hai. Tuy nhiên, vô tình huống cần thiết xác lập khoảng cách từ 1 điểm bên trên một đường thẳng liền mạch cho tới đường thẳng liền mạch sót lại (không cần bên trên nút giao nhau), chúng ta cũng có thể vận dụng công thức tính khoảng cách kể từ điểm đến chọn lựa lối thẳng:
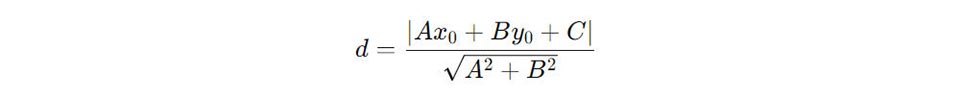
Trong đó:
- A, B, C là thông số của phương trình đường thẳng liền mạch.
- (x0, y0) là tọa chừng của điểm bên trên đường thẳng liền mạch cơ.
Cách tính khoảng cách đằm thắm hai tuyến phố trực tiếp vô ko gian
Tương tự động, nhằm biết phương pháp tính khoảng cách đằm thắm hai tuyến phố trực tiếp vô không khí, chúng ta cần phải biết hiểu cách thức phân biệt trong những đường thẳng liền mạch tuy vậy tuy vậy, rời nhau và chéo cánh nhau, kể từ cơ vận dụng công thức tương thích nhằm đo lường.
1. Phân biệt đằm thắm đường thẳng liền mạch tuy vậy tuy vậy, rời nhau và chéo cánh nhau
Dưới đấy là một vài ba khêu ý giản dị sẽ giúp đỡ chúng ta cũng có thể phân biệt đằm thắm đường thẳng liền mạch tuy vậy tuy vậy, rời nhau và chéo cánh nhau vô ko gian:
- Đường trực tiếp tuy vậy song: Trong không khí, hai tuyến phố trực tiếp tuy vậy song ko lúc nào giao phó nhau và khoảng cách đằm thắm bọn chúng luôn luôn thắt chặt và cố định. Chúng với nằm trong phương và ko nằm trong địa điểm.
- Đường trực tiếp rời nhau: Hai đường thẳng liền mạch rời nhau là lúc bọn chúng giao phó nhau bên trên một điểm có một không hai vô không khí. Trường thích hợp này sẽ không cần thiết tính khoảng cách vì thế nút giao đó là khoảng cách bởi vì 0.
- Đường trực tiếp chéo cánh nhau: Hai đường thẳng liền mạch chéo cánh nhau là lúc bọn chúng ko nằm trong và một mặt mũi phẳng lặng và ko giao phó nhau. Khoảng cơ hội đằm thắm bọn chúng được xem trải qua đoạn vuông góc công cộng đằm thắm hai tuyến phố.
2. Công thức tính khoảng cách đằm thắm hai tuyến phố trực tiếp tuy vậy song
Khoảng cơ hội đằm thắm hai tuyến phố trực tiếp tuy vậy song vô không khí rất có thể được xem tương tự động như vô mặt mũi phẳng lặng, bởi vì công thức:
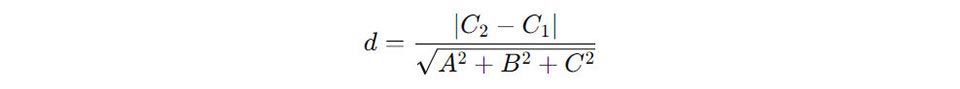
Trong đó:
- A, B, C là thông số của phương trình tổng quát mắng của hai tuyến phố trực tiếp tuy vậy tuy vậy.
- C1, C2 là thông số tự tại vô phương trình của hai tuyến phố trực tiếp.
3. Công thức tính khoảng cách đằm thắm hai tuyến phố trực tiếp chéo cánh nhau
Khoảng cơ hội đằm thắm hai tuyến phố trực tiếp chéo cánh nhau vô không khí được xem bởi vì đoạn vuông góc công cộng đằm thắm bọn chúng. Cụ thể, vô hệ tọa chừng Oxyz, công thức tính khoảng cách giữa hai đường thẳng chéo cánh nhau là:
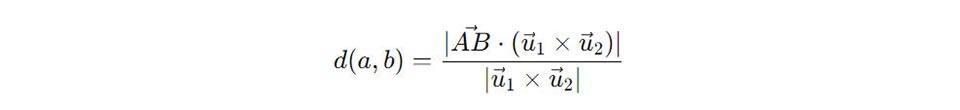
Trong đó:
- u→1 và u→2 là những vectơ chỉ phương của hai tuyến phố trực tiếp.
- AB→ là vectơ nối từ 1 điểm bên trên đường thẳng liền mạch loại nhất cho tới một điểm bên trên đường thẳng liền mạch loại nhì.
Dấu “⋅” biểu thị tích vô phía, còn “×” biểu thị tích với hướng
Phương pháp này khiến cho bạn dễ dàng và đơn giản đo lường khoảng cách đằm thắm hai tuyến phố trực tiếp chéo cánh nhau bằng phương pháp dùng những vectơ và tích được đặt theo hướng. Nó cực kỳ hữu ích vô không khí phụ thân chiều.
Tạm kết
Việc nắm rõ phương pháp tính khoảng cách đằm thắm hai tuyến phố trực tiếp vô hình học tập phẳng lặng và không khí tiếp tục khiến cho bạn dễ dàng và đơn giản xử lý những câu hỏi học tập thuật. Dường như, chúng ta còn rất có thể vận dụng nó vô những phần mềm thực tiễn biệt như design phong cách thiết kế hoặc phân tích khoa học tập. Qua nội dung bài viết này, FPT Shop kỳ vọng chúng ta tiếp tục làm rõ rộng lớn về những công thức và cách thức tính nhằm sẵn sàng phần mềm trong mỗi câu hỏi phức tạp rộng lớn.
Nếu chúng ta đang được cần thiết mua sắm máy tính xách tay mới mẻ nhằm tiếp thu kiến thức hoặc thao tác làm việc, hãy truy vấn vô lối links bên dưới hoặc ghé thăm hỏi những cửa hàng sớm nhất của FPT Shop nhé.
- Laptop chủ yếu hãng
Xem thêm:
- Tổng quan tiền về công thức nguyên vẹn hàm và cơ hội ghi lưu giữ toàn bộ chỉ vô vài ba phút
- Tìm hiểu công thức tính công cơ học tập chuẩn chỉnh xác và những kỹ năng cần thiết nên biết